Método dos deslocamentos
Simular uma placa através de elementos de barras formando uma grelha, é um procedimento conhecido desde os primórdios da engenharia estrutural. A Analogia de Grelha foi usada por Euler em 1766 para a solução de problemas de membranas elásticas e por Hrennikoff em 1941 para a análise de placas através de uma formulação denominada Lattice Analogy.
Método dos deslocamentos
O método dos deslocamentos, também conhecido como método da rigidez, é um método de análise de estruturas reticuladas que usa a rigidez dos elementos para formar um sistema de equações, relacionando os deslocamentos com as cargas que atuam na estrutura. A equação básica do método é:
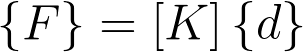
Onde:
-
{F} é uma matriz coluna (um vetor) das cargas externas;
-
[K] é a matriz de rigidez da estrutura;
-
{d} é a matriz coluna dos deslocamentos.
Para um dado conjunto de cargas externas, o sistema de equações é resolvido calculando-se os deslocamentos. Os esforços nas barras da estrutura são obtidos com base nos deslocamentos e nas matrizes de rigidez de cada elemento isolado. O método da rigidez é um método muito geral que pode ser aplicado à resolução de qualquer tipo de estrutura reticulada. A análise de uma estrutura pelo método da rigidez pode ser descrita pelas seguintes etapas, conforme GERE e WEAVER (1980):
- A descrição da estrutura inclui o tipo de estrutura, a localização dos nós, posições das barras bem como a localização e tipos de apoios.
- Especificação dos tipos de deformação a serem consideradas na análise, tais como deformações por flexão e deformações axiais. Dependendo dos tipos de deformações a serem consideradas, deve ser dado às barras a rigidez apropriada.
- Determinação do número de deslocamentos de nós desconhecidos ou graus de liberdade na estrutura. Há que se proporcionar um número correspondente de vínculos artificiais para produzir a estrutura restringida, na qual todos os deslocamentos de nós são nulos.
- Análise da estrutura restringida submetida às cargas. Todas as cargas, exceto aquelas correspondentes a um deslocamento de nó desconhecido, são consideradas como aplicadas à estrutura fixa, sendo avaliadas as várias ações na estrutura. As ações mais importantes a serem determinadas são as ações que correspondem aos deslocamentos desconhecidos. Outras ações de interesse são as ações de extremidade para os membros e as reações nos apoios.
- Análise da estrutura restringida por outras causas.
- Análise da estrutura restringida para valores unitários dos deslocamentos.
- Determinação dos deslocamentos.
A equação de superposição para as ações correspondentes aos deslocamentos na estrutura real é:
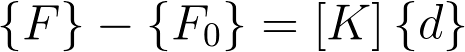
,onde {F} representa os esforços nos nós, enquanto que {F0} representa os esforços de imobilização dos nós, devidos aos carregamentos aplicados nas barras. Nesta equação, o vetor {F0} inclui os efeitos de cargas, variações de temperatura, deformações iniciais e deslocamentos de apoio. Quando se resolve a equação de superposição em função dos deslocamentos, o resultado é:
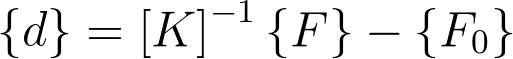
Os vetores para as ações de extremidade de membro e reações, respectivamente, na estrutura real são obtidos das seguintes equações de superposição:
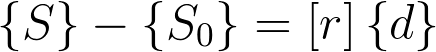
Quando os vetores {S},{S0} e {d} tiverem sido obtidos, a análise pode ser considerada completa. No próximo artigo desta série, Método dos deslocamentos aplicado a grelhas planas, irei mostrar como este método se aplica a grelhas planas.
![Brand Vertical-PRINCIPAL-1.png]](https://suporte.altoqi.com.br/hs-fs/hubfs/Brand%20Vertical-PRINCIPAL-1.png?width=70&height=63&name=Brand%20Vertical-PRINCIPAL-1.png)