Instabilidade lateral em vigas de concreto armado
Quando vigas esbeltas são usadas, a instabilidade lateral pode ser, em alguns casos, a causa do esgotamento da capacidade resistente da peça, antes que seja atingido o estado limite último por flexão. Por conta disto, é interessante que este fenômeno seja verificado.
Instabilidade lateral em vigas de concreto armado
O colapso por instabilidade lateral é acompanhado por uma rotação da viga, conforme mostrado na figura abaixo. Em linhas gerais, a parte comprida da viga está propensa a uma instabilidade análoga à flambagem em pilares. Isto faz com que a viga rotacione, diminuindo a sua capacidade portante.
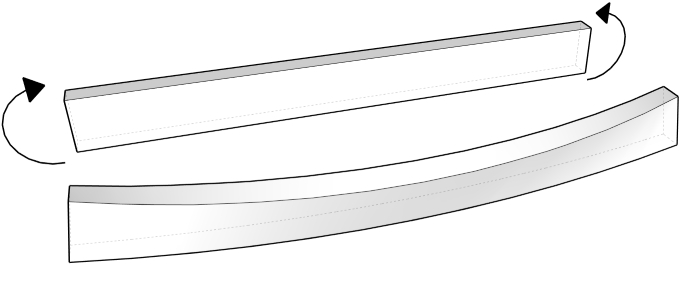
O fenômeno da instabilidade lateral pode ser importante no caso de vigas com insuficiência de travamento lateral, quando a rigidez à flexão no plano vertical (Mx) é muito maior se comparada com a rigidez lateral. A ocorrência deste fenômeno é minimizada pelo fato de que geralmente a zona comprimida das vigas está travada por lajes ou mesmo por vigas.
Cálculo do momento crítico Mcr
Um tratamento analítico para o cálculo do momento crítico que resulta em instabilidade lateral se tornaria muito complexo se fossem avaliadas todas as características que influenciam o comportamento realista das vigas de concreto armado. Como há poucos estudos experimentais comprovando a teoria derivada de cargas críticas, fica difícil quantificar quais são esses parâmetros relevantes no processo.
MICHELL´S (1899) propôs uma solução clássica para o momento crítico Mcr, que produz instabilidade lateral em uma viga de material isotrópico, elástico linear e homogêneo, mostrada abaixo:
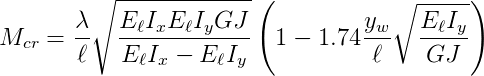
onde:

MARSHALL (1969) estudou a aplicabilidade de cada termo da equação para vigas de concreto armado, procurando estabelecer limites dentro dos quais é mais provável que o momento crítico ocorra. As seções transversais que são sensíveis à instabilidade lateral tem a relação altura/largura pelo menos igual a 2. Além disso, se o efeito da fissuração for levado em consideração, a razão Iy/Ix torna-se pequena e pode chegar a zero. Com esta simplificação, a equação acima é reduzida para:
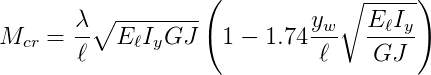
Na avaliação do momento crítico, alguns pontos devem ser analisados:
-
O primeiro deles diz respeito ao comportamento não linear do concreto armado. Isto leva a considerações especiais no módulo de elasticidade Ec como também no cálculo do momento de inércia, que é função do grau de fissuração desse material;
-
O módulo de rigidez transversal "G" está relacionado ao módulo de elasticidade longitudinal Ec. No entanto, a contribuição efetiva do concreto quando solicitado a torção, neste caso, ainda é incerta e controversa.
Partindo das premissas acima, é evidente que há dificuldades em estimar adequadamente os parâmetros de rigidez. Substituindo yw por 0.5h na equação acima, considerando a não linearidade física do concreto como sendo uma parcela da resistência característica do concreto f'c e expressando Ix, Iy e J em função das dimensões do elemento, a equação do momento crítico para uma viga retangular reduz-se a:
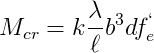
onde:

A NBR 6118:2007 no item 8.2.8, prescreve a utilização do módulo de elasticidade secante Ecs para a determinação dos esforços solicitantes e verificação dos estados limites de serviço, tomado como uma parcela do módulo de elasticidade inicial Eci, sendo Ecs = 0.85Eci, onde Eci = 5600 fck1/2,quando não forem feitos ensaios e não existirem dados mais precisos para sua determinação.
Apesar de haver diferenças na formulação dos valores de f´c e fck nas normas do ACI-318 e NBR 6118:2014 (ver VASCONCELOS (1993)), neste artigo será adotado fck no lugar de f´c. Portanto, a equação acima torna-se:
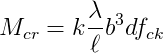

Para que ocorra o fenômeno da instabilidade lateral em vigas, é necessário que a resistência a flexão da viga Mu seja maior que o momento crítico Mcr. Caso contrário, a flexão será preponderante. A capacidade a flexão da viga depende, dentre outros fatores, da quantidade de aço contida na seção transversal, que, para uma seção simplesmente armada estão entre os limites de:
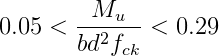
Considerando vigas com máximas taxas de armaduras permitidas, a condição crítica é aproximadamente:
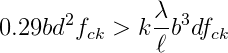
ou simplesmente:
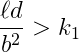
onde:
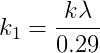
Criando limites aceitáveis para as variáveis, o valor de k1 fica dentro do intervalo de 100 a 580 para vigas com cargas uniformemente distribuídas. Dados esses limites, maiores refinamentos da análise levando em consideração a contribuição à flexão do aço não é garantida. Examinando dados experimentais disponíveis, MARSHALL (1969) concluiu que a maioria dos valores encontrados para ld/b2 estavam mais próximos do limite de 580.
Vale frisar que a tradicional relação vão/largura (l/b), quando utilizada isoladamente, não descreve adequadamente o critério de instabilidade em vigas. Além disso, o efeito da deformação lenta e a falta de ductilidade aumentam o grau de incertezas na determinação do momento crítico Mcr. No artigo Aviso 26 - Possibilidade de instabilidade lateral, é abordado estes critérios aplicados ao AltoQi Eberick.
![Brand Vertical-PRINCIPAL-1.png]](https://suporte.altoqi.com.br/hs-fs/hubfs/Brand%20Vertical-PRINCIPAL-1.png?width=70&height=63&name=Brand%20Vertical-PRINCIPAL-1.png)