---
title: "Faixas de Hillerborg: aplicação"
description: Neste artigo, será abordado o método de Hillerborg para o cálculo de lajes. Diversos métodos aproximados de análise de lajes têm sido propostos, desenvolvidos e usados ao longo dos anos. Entre eles, e
---
[Pular para o conteúdo](https://suporte.altoqi.com.br/hc/pt-br/articles/360003606054#main-content)
[![Brand Vertical-PRINCIPAL-1.png\]](https://suporte.altoqi.com.br/hs-fs/hubfs/Brand%20Vertical-PRINCIPAL-1.png?width=70&height=63&name=Brand%20Vertical-PRINCIPAL-1.png)](https://suporte.altoqi.com.br/hc/pt-br)
Abrir navegação principal
Fechar navegação principal
- [Área do cliente](https://areacliente.altoqi.com.br/)
[Área do cliente](https://areacliente.altoqi.com.br/)
Como podemos ajudar?
- Não há sugestões porque o campo de pesquisa está em branco.
1. [AltoQi Suporte](https://suporte.altoqi.com.br/hc/pt-br)
2. [AltoQi Eberick](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick)
3. [Lajes | Dimensionamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#lajes-dimensionamento)
22 de março de 2024
# Faixas de Hillerborg: aplicação
Neste artigo, será abordado o método de Hillerborg para o cálculo de lajes. Diversos métodos aproximados de análise de lajes têm sido propostos, desenvolvidos e usados ao longo dos anos. Entre eles, está o conhecido método das faixas, apresentado por Hillerborg em 1956. Esse procedimento pode ser usado para determinar a distribuição de esforços e possibilitar o dimensionamento das seções de concreto e das armaduras de um sistema de lajes.
### Análise de lajes pelo método das faixas de Hillerborg: aplicação
O método da análise limite inferior foi chamado de “teoria do equilíbrio” por HILLERBORG (1956) e sugerido por ele como um método de projeto para lajes de concreto armado. O método de projeto pode ser resumido no seguinte, conforme Hillerborg:
*“Se uma distribuição de momentos pode ser encontrada de tal modo que satisfaça as equações de equilíbrio e as condições de contorno da placa para uma determinada carga externa, e se a placa é capaz de resistir a esses momentos em cada ponto, então a carga externa adotada representa um limite inferior da capacidade de suporte da placa”.*
O objetivo de Hillerborg era apresentar um método de projeto que fosse ao mesmo tempo simples de ser aplicado e que apresentasse sempre resultados a favor da segurança. De certo modo, o seu objetivo foi alcançado; o método é simples e resulta em dimensionamentos sempre a favor da segurança. Este método vem sendo usado por engenheiros de projeto há muitos anos, e, em muitos casos, até de forma intuitiva, desconhecendo o fato de que estão usando um método formulado em bases formais.
O método das faixas também foi tratado em outras publicações como CRAWFORD(1962), WOOD e ARMER (1968), KEMP (1970,1971 ), SHUKLA (1973) e outros. Wood e Armer tornaram o método das faixas muito mais poderoso com a introdução do conceito de **faixas reforçadas** (strong bands), para possibilitar o cálculo de pavimentos sem vigas apoiados em pilares e lajes com bordos livres e aberturas.
Um ponto em comum deste método com o das charneiras plásticas é o fato de que a distribuição dos momentos nas duas direções é deixada para o engenheiro. Essa liberdade, no entanto, deve levar em consideração o fato que, se usada sem nenhum cuidado, pode levar ao cálculo de lajes que, embora satisfaçam os requisitos de resistência, apresentam problemas com relação ao comportamento em serviço, com fissuras ou flechas excessivas. Essa liberdade também pode levar a soluções que requeiram uma grande redistribuição de esforços para atingir a carga última, e que necessitam então de uma extrema ductilidade das seções de concreto. Portanto, o engenheiro quando usar esse método precisa distribuir os momentos em proporções próximas daquelas obtidas pela teoria elástica.
É importante notar que a distribuição de momentos obtida pela teoria elástica para uma placa é, de fato, uma solução possível de estado limite inferior pois ela satisfaz as condições de equilíbrio, as condições de contorno e as seções da placa são dimensionadas para resistir com segurança aos momentos em cada ponto.
Hillerborg simplificou o método geral do limite inferior eliminando a necessidade de se considerar os momentos de torção no cálculo da distribuição de momentos. Se nenhuma parcela de carga é absorvida pelos momentos de torção, o dimensionamento pode ser feito como se a laje fosse composta de faixas independentes, em geral nas duas direções. Torna-se necessário apenas calcular os momentos das faixas por critérios de estática, garantindo o equilíbrio. Esta simplificação resultou em um método extremamente atrativo para a área de projeto. O método foi chamado de método simples das faixas. Posteriormente foi apresentado por Hillerborg o método avançado das faixas, para enquadrar casos especiais de lajes apoiadas em pilares.
Hillerborg propõe que a distribuição de momentos em equilíbrio com o carregamento externo, seja obtida desprezando os momentos volventes. Neste caso, a equação pode ser escrita:
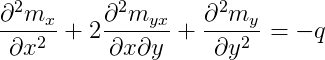
Essa expressão pode ser decomposta em duas:
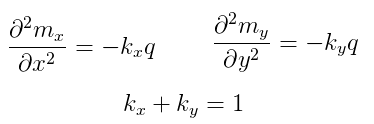
As equações acima correspondem ao funcionamento de vigas nas direções **x** e **y**. Portanto, a laje pode ser calculada como se fossem faixas de vigas nas direções **x** e **y**, distribuindo-se adequadamente o carregamento para essas faixas e utilizando condições de vinculação adequadas.
Para ilustrar o uso do método, serão calculados dois exemplos apresentados por HILLERBORG, PARK e GAMBLE (1980) - de uma laje quadrada, simplesmente apoiada em todo o contorno submetida a um carregamento uniformemente distribuído. Os carregamentos e as dimensões foram alterados por conveniência deste artigo.
#### Exemplo 1 Laje quadrada com 4x4m
Carga distribuída **q** de 1000 kgf/m2, com uma distribuição de faixas conforme mostrado na figura abaixo. Pode-se encontrar uma distribuição de momentos em equilíbrio fazendo Kx = 0,5. Deste modo, metade da carga será distribuída uniformemente para as faixas em cada direção. O resultado dos momentos obtidos para as faixas na direção X é dado pelo cálculo estático de uma viga biapoida com largura unitária. O valor máximo dos momentos na direção x é:
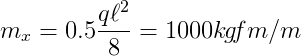
As reações nos apoios também podem ser obtidas por estática:
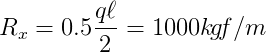
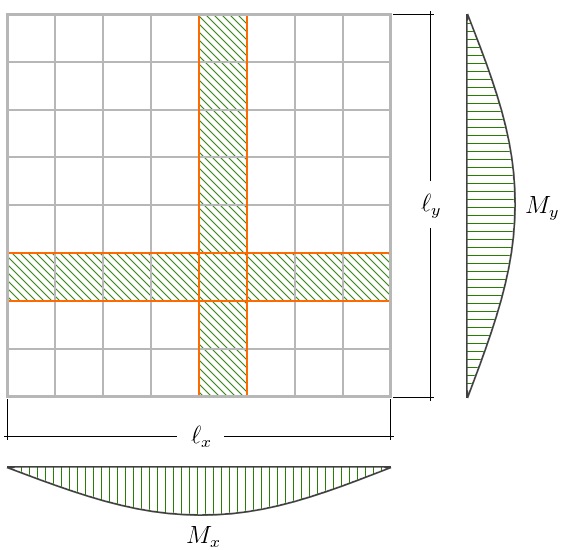
Todas as faixas possuem o mesmo diagrama de momentos fletores e a laje precisa ser dimensionada de modo a respeitar esse diagrama em todas os pontos.
#### Exemplo 2 – Laje quadrada com 4x4m
Carga distribuída q de 1000 kgf/m2 com uma distribuição de faixas, conforme mostrado na figura abaixo. Pode-se encontrar uma distribuição de momentos em equilíbrio adotando para Kx valores 0 ou 1 dependendo da região da laje em que se encontra a faixa. A carga é dividida em regiões triangulares que transmitem a carga para o apoio mais próximo. Cada faixa carrega toda a carga distribuída q apenas nas extremidades de comprimento. O valor do momento máximo das faixas na direção x é uma função de y , apresenta um valor máximo na faixa central e valores decrescentes em direção ao apoio de maneira não-linear conforme mostrado no gráfico. O valor máximo da faixa central é:
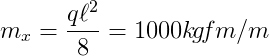
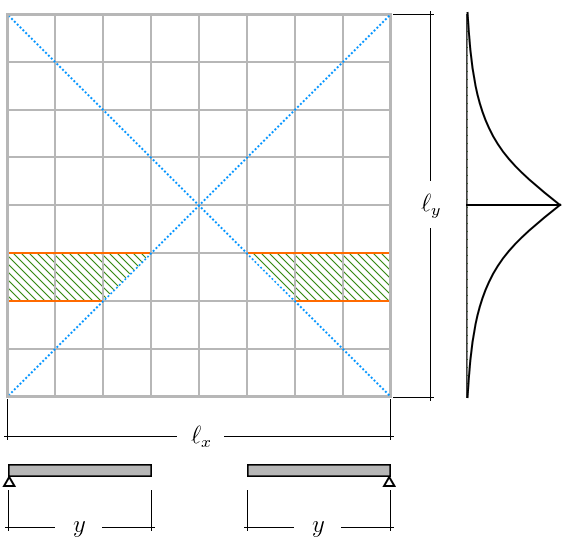
Para a mesma laje, o método de Hillerborg permite inúmeras outras soluções, como, por exemplo, o caso extremo onde, com o valor Kx =1, toda a carga distribuída seria absorvida apenas na direção lx. A escolha entre todas as soluções possíveis passa a ser, portanto, um problema de otimização de detalhamento e custo das armaduras, que seriam dispostas de acordo com os diagramas de momentos. Na prática, uma solução como a do exemplo 2 mostra-se impraticável devido ao corte ou ao espaçamento variável de todas as barras da armadura.
Os exemplos demonstram a simplicidade e a facilidade com que os momentos de uma laje podem ser encontrados com a simples aplicação da estática e a diversidade de soluções possíveis para uma mesma laje.
É interessante salientar que muitos projetistas têm utilizado o método das faixas para calcular de modo aproximado lajes que apresentam formatos irregulares, aberturas, bordos livres e diversas outras situações não encontradas nas soluções clássicas e nas tabelas. Faziam, e em muitos casos ainda fazem, sem saber que estão utilizando um método com um suporte formal no método do estado limite inferior. No próximo artigo dessa série, Faixas de Hillerborg: faixas reforçadas, irei mostrar como isto pode ser feito com o conceito de faixas reforçadas.
- [Instalação, Ativação e Área do Cliente](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#main-content)
- [Requisitos de Sistema Operacional e Compatibilidade](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#requisitos-de-sistema-operacional-e-compatibilidade)
- [Firewall, Proxy e Antivírus](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#firewall-proxy-e-antivírus)
- [Recursos Gráficos e Placa de Vídeo](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#recursos-gráficos-e-placa-de-vídeo)
- [Instalação & Acesso por Login Integrado](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#instalação-acesso-por-login-integrado)
- [Versões demonstrativas](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#versões-demonstrativas)
- [Instalação & Acesso por Chave de Ativação EID | Em migração](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#instalação-acesso-por-chave-de-ativação-eid-em-migração)
- [Versões anteriores](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#versões-anteriores)
- [Outros](https://suporte.altoqi.com.br/hc/pt-br/instala%C3%A7%C3%A3o-ativa%C3%A7%C3%A3o-e-%C3%A1rea-do-cliente#outros)
- [AltoQi Education](https://suporte.altoqi.com.br/hc/pt-br/altoqi-education)
- [Novidades de Release](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#main-content)
- [Atualizações AltoQi Builder](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-builder)
- [Atualizações AltoQi Eberick](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-eberick)
- [Atualizações AltoQi Visus](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-visus)
- [Atualizações AltoQi Visus Cost Management](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-visus-cost-management)
- [Atualizações AltoQi Visus Collab](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-visus-collab)
- [Atualizações AltoQi Visus WorkFlow](https://suporte.altoqi.com.br/hc/pt-br/novidades-de-release#atualizações-altoqi-visus-workflow)
- [Quero falar com o Suporte](https://suporte.altoqi.com.br/hc/pt-br/quero-falar-com-o-suporte#main-content)
- [Atendimento de Suporte ao Produto](https://suporte.altoqi.com.br/hc/pt-br/quero-falar-com-o-suporte#atendimento-de-suporte-ao-produto)
- [Envio de inconsistências (bugs), melhorias e sugestões](https://suporte.altoqi.com.br/hc/pt-br/quero-falar-com-o-suporte#envio-de-inconsistências-bugs-melhorias-e-sugestões)
- [Envio de anexos](https://suporte.altoqi.com.br/hc/pt-br/quero-falar-com-o-suporte#envio-de-anexos)
- [Arquitetura e Interoperabilidade BIM](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#main-content)
- [Preparação da Arquitetura](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#preparação-da-arquitetura)
- [Interoperabilidade BIM](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#interoperabilidade-bim)
- [Colaboração BIM](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#colaboração-bim)
- [Exportação e Importação de Modelos 3D (formato Q3D)](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#exportação-e-importação-de-modelos-3d-formato-q3d)
- [Integração com Revit](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#integração-com-revit)
- [Visualização em Realidade Aumentada (RA)](https://suporte.altoqi.com.br/hc/pt-br/arquitetura-e-interoperabilidade-bim#visualização-em-realidade-aumentada-ra)
- [AltoQi Visus](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#main-content)
- [Plataforma AltoQi Visus](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#plataforma-altoqi-visus)
- [Cost Management](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#cost-management)
- [Planning](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#planning)
- [Collab](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#collab)
- [Workflow](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#workflow)
- [Bid](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#bid)
- [Tracking](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#tracking)
- [Control Tower](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus#control-tower)
- [AltoQi Builder](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#main-content)
- [Interface](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#interface)
- [Criação, abertura e salvamento de projetos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#criação-abertura-e-salvamento-de-projetos)
- [Arquitetura e Desenhos Base | Base 2D](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#arquitetura-e-desenhos-base-base-2d)
- [Arquitetura e Desenhos Base | Interoperabilidade BIM (arquivos IFC e referências 3D externas)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#arquitetura-e-desenhos-base-interoperabilidade-bim-arquivos-ifc-e-referências-3d-externas)
- [Arquitetura e Desenhos Base | Recursos de CAD (ferramentas de desenho)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#arquitetura-e-desenhos-base-recursos-de-cad-ferramentas-de-desenho)
- [Projetos Multidisciplinares e Integração entre Disciplinas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#projetos-multidisciplinares-e-integração-entre-disciplinas)
- [Visualização do Projeto e Níveis de Desenho](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#visualização-do-projeto-e-níveis-de-desenho)
- [Pavimentos e Níveis de Projeto](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#pavimentos-e-níveis-de-projeto)
- [Cadastro](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#cadastro)
- [Simbologias](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#simbologias)
- [Condutos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#condutos)
- [Peças, Conexões e Elementos Genéricos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#peças-conexões-e-elementos-genéricos)
- [Avisos e Indicações](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#avisos-e-indicações)
- [Colunas e Prumadas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#colunas-e-prumadas)
- [Geral](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#geral)
- [Disciplina Cabeamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-cabeamento)
- [Disciplina Alvenaria](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-alvenaria)
- [Disciplina Climatização](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-climatização)
- [Disciplina Elétrico | Pontos elétricos e comandos (lâmpadas, interruptores, tomadas, comandos)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-elétrico-pontos-elétricos-e-comandos-lâmpadas-interruptores-tomadas-comandos)
- [Disciplina Elétrico | Sistemas Fotovoltaicos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-elétrico-sistemas-fotovoltaicos)
- [Disciplina Gás](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-gás)
- [Disciplina Hidráulico | Reservatórios (caixa d'água)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-reservatórios-caixa-dágua)
- [Disciplina Hidráulico | Alimentação, hidrômetros (coletivos e individuais) e bombas de recalque](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-alimentação-hidrômetros-coletivos-e-individuais-e-bombas-de-recalque)
- [Disciplina Hidráulico | Colunas, Prumadas e Barriletes de Distribuição](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-colunas-prumadas-e-barriletes-de-distribuição)
- [Disciplina Hidráulico | Condutos (tubulações) e lançamentos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-condutos-tubulações-e-lançamentos)
- [Disciplina Hidráulico | Ramais e Ambientes Molhados (banheiros, cozinhas, áreas de serviço)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-ramais-e-ambientes-molhados-banheiros-cozinhas-áreas-de-serviço)
- [Disciplina Hidráulico | Peças e materiais (PEX, registros, conexões)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-peças-e-materiais-pex-registros-conexões)
- [Disciplina Hidráulico | Aquecedores, Reservatórios Térmicos e Placas Solares](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-aquecedores-reservatórios-térmicos-e-placas-solares)
- [Disciplina Hidráulico | Piscinas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-piscinas)
- [Disciplina Hidráulico | Verificação de pressões, vazões e perdas de carga](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-verificação-de-pressões-vazões-e-perdas-de-carga)
- [Disciplina Hidráulico | Soluções para pressão (pressurizadores e VRP)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-hidráulico-soluções-para-pressão-pressurizadores-e-vrp)
- [Disciplina Sanitário | Colunas Sanitárias, Ventilação e Tubos de Queda](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-colunas-sanitárias-ventilação-e-tubos-de-queda)
- [Disciplina Sanitário | Ramais e Ambientes Sanitários (banheiros, cozinhas, áreas de serviço)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-ramais-e-ambientes-sanitários-banheiros-cozinhas-áreas-de-serviço)
- [Disciplina Sanitário | Peças e componentes (ralos, sifões, conexões)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-peças-e-componentes-ralos-sifões-conexões)
- [Disciplina Sanitário | Caixas de passagem, gordura e sifonadas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-caixas-de-passagem-gordura-e-sifonadas)
- [Disciplina Sanitário | Rede Pluvial, Calhas e Coletores](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-rede-pluvial-calhas-e-coletores)
- [Disciplina Sanitário | Unidades de Tratamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-unidades-de-tratamento)
- [Disciplina Sanitário | Estações elevatórias e bombas submersíveis](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-estações-elevatórias-e-bombas-submersíveis)
- [Disciplina Sanitário | Verificações e dimensionamento (diâmetros, declividades, inclinações)](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-sanitário-verificações-e-dimensionamento-diâmetros-declividades-inclinações)
- [Disciplina Incêndio | Configurações, normas e mensagens gerais](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-configurações-normas-e-mensagens-gerais)
- [Disciplina Incêndio | Bombas de Incêndio](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-bombas-de-incêndio)
- [Disciplina Incêndio | Sprinklers: lançamento, critérios e dimensionamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-sprinklers-lançamento-critérios-e-dimensionamento)
- [Disciplina Incêndio | Hidrantes e mangotinhos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-hidrantes-e-mangotinhos)
- [Disciplina Incêndio | Planilha de Pressão, perdas de carga e comportamento hidráulico](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-planilha-de-pressão-perdas-de-carga-e-comportamento-hidráulico)
- [Disciplina Incêndio | Sinalização, preventivo e equipamentos auxiliares](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-incêndio-sinalização-preventivo-e-equipamentos-auxiliares)
- [Disciplina SPDA](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#disciplina-spda)
- [Relatórios](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#relatórios)
- [Visão 3D](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#visão-3d)
- [Cortes, detalhes e esquemas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#cortes-detalhes-e-esquemas)
- [Pranchas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#pranchas)
- [Controle de revisões](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#controle-de-revisões)
- [Impressão e Exportação](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#impressão-e-exportação)
- [Outros](https://suporte.altoqi.com.br/hc/pt-br/altoqi-builder#outros)
- [AltoQi Eberick](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#main-content)
- [Interface](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#interface)
- [Criação, abertura e salvamento de projetos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#criação-abertura-e-salvamento-de-projetos)
- [Pavimentos e níveis intermediários](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#pavimentos-e-níveis-intermediários)
- [Desenhos e Arquitetura](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#desenhos-e-arquitetura)
- [Desenhos e Arquitetura | Interoperabilidade BIM](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#desenhos-e-arquitetura-interoperabilidade-bim)
- [Pilares | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#pilares-lançamento)
- [Pilares | Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#pilares-erros-e-avisos)
- [Pilares | Dimensionamento e Detalhamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#pilares-dimensionamento-e-detalhamento)
- [Vigas | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#vigas-lançamento)
- [Vigas | Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#vigas-erros-e-avisos)
- [Vigas | Dimensionamento e Detalhamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#vigas-dimensionamento-e-detalhamento)
- [Lajes | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#lajes-lançamento)
- [Lajes | Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#lajes-erros-e-avisos)
- [Lajes | Dimensionamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#lajes-dimensionamento)
- [Lajes | Detalhamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#lajes-detalhamento)
- [Fundações | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#fundações-lançamento)
- [Fundações | Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#fundações-erros-e-avisos)
- [Fundações | Dimensionamento e Detalhamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#fundações-dimensionamento-e-detalhamento)
- [Cargas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#cargas)
- [Escadas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#escadas)
- [Escadas | Exemplos de Lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#escadas-exemplos-de-lançamento)
- [Reservatórios](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#reservatórios)
- [Reservatórios | Exemplos de lançamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#reservatórios-exemplos-de-lançamento)
- [Paredes de contenção](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#paredes-de-contenção)
- [Muros de Arrimo](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#muros-de-arrimo)
- [Elementos genéricos e perfis metálicos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#elementos-genéricos-e-perfis-metálicos)
- [Estruturas de Alvenaria Estrutural](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#estruturas-de-alvenaria-estrutural)
- [Estruturas de Protensão](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#estruturas-de-protensão)
- [Estruturas Pré-Moldadas](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#estruturas-pré-moldadas)
- [Estruturas Pré-Moldadas | Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#estruturas-pré-moldadas-erros-e-avisos)
- [Processamento](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#processamento)
- [Análise da estrutura](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#análise-da-estrutura)
- [Estabilidade global](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#estabilidade-global)
- [Deslocamentos e durabilidade](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#deslocamentos-e-durabilidade)
- [Planta de fôrma e locação](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#planta-de-fôrma-e-locação)
- [Pranchas e detalhamentos](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#pranchas-e-detalhamentos)
- [Configurações](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#configurações)
- [Outros](https://suporte.altoqi.com.br/hc/pt-br/altoqi-eberick#outros)
- [Editor de Armaduras](https://suporte.altoqi.com.br/hc/pt-br/editor-de-armaduras#main-content)
- [Pranchas e detalhamentos](https://suporte.altoqi.com.br/hc/pt-br/editor-de-armaduras#pranchas-e-detalhamentos)
- [Integração com o Eberick](https://suporte.altoqi.com.br/hc/pt-br/editor-de-armaduras#integração-com-o-eberick)
- [Configurações](https://suporte.altoqi.com.br/hc/pt-br/editor-de-armaduras#configurações)
- [Resumo de materiais](https://suporte.altoqi.com.br/hc/pt-br/editor-de-armaduras#resumo-de-materiais)
- [Elétrico](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#main-content)
- [Módulo Fotovoltaico](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#módulo-fotovoltaico)
- [Cadastro](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#cadastro)
- [Lâmpadas e comandos | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#lâmpadas-e-comandos-lançamento)
- [Tomadas | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#tomadas-lançamento)
- [Quadros | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#quadros-lançamento)
- [Pontos em geral | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#pontos-em-geral-lançamento)
- [Condutos | Lançamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#condutos-lançamento)
- [Quadros | Operações](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#quadros-operações)
- [Circuitos | Operações](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#circuitos-operações)
- [Condutos | Operações](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#condutos-operações)
- [Fiação | Operações](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#fiação-operações)
- [Fiação | Configurações](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#fiação-configurações)
- [Dimensionamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#dimensionamento)
- [Erros de dimensionamento](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#erros-de-dimensionamento)
- [Erros e Avisos](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#erros-e-avisos)
- [Quadros e Diagramas | Detalhamentos](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#quadros-e-diagramas-detalhamentos)
- [Legendas e Relatórios | Detalhamentos](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#legendas-e-relatórios-detalhamentos)
- [Outros](https://suporte.altoqi.com.br/hc/pt-br/el%C3%A9trico#outros)
- [AltoQi Visus Cost Management](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus-cost-management#main-content)
- [Versões AltoQi Visus Cost Management](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus-cost-management#versões-altoqi-visus-cost-management)
- [Licença do AltoQi Visus Cost Management](https://suporte.altoqi.com.br/hc/pt-br/altoqi-visus-cost-management#licença-do-altoqi-visus-cost-management)
- [Blog](https://blog.altoqi.com.br/?_gl=1*1g9eywx*_gcl_au*NjY4MjI3ODQwLjE3NTkzMzAwNTcuNTI2MzMzOTU0LjE3NjIxOTQwNzcuMTc2MjE5NDExMA..*_ga*MTA2NDI3ODc1Ny4xNzYyMTkyMTE4*_ga_YWTWJ4QJW7*czE3NjIxOTIxMTgkbzckZzEkdDE3NjIyMDIwNTQkajIyJGwwJGgw*_ga_MSCRTLB9RC*czE3NjIxOTIxMTgkbzExJGcxJHQxNzYyMjAyMDU0JGoyMiRsMCRoMA..)
- [Conteúdos Gratuitos](https://www.altoqi.com.br/conteudos-gratuitos?_gl=1*1g9eywx*_gcl_au*NjY4MjI3ODQwLjE3NTkzMzAwNTcuNTI2MzMzOTU0LjE3NjIxOTQwNzcuMTc2MjE5NDExMA..*_ga*MTA2NDI3ODc1Ny4xNzYyMTkyMTE4*_ga_YWTWJ4QJW7*czE3NjIxOTIxMTgkbzckZzEkdDE3NjIyMDIwNTQkajIyJGwwJGgw*_ga_MSCRTLB9RC*czE3NjIxOTIxMTgkbzExJGcxJHQxNzYyMjAyMDU0JGoyMiRsMCRoMA..)
- [Canais de Atendimento AltoQi](https://suporte.altoqi.com.br/hc/pt-br/nossos-canais-de-atendimento)
- [Como funciona o Suporte Técnico AltoQi?](https://suporte.altoqi.com.br/hc/pt-br/atendimento-setup-e-suporte-altoqi)
- [Como relato um problema ou inconsistência?](https://suporte.altoqi.com.br/hc/pt-br/articles/360002961233)
- [Política de Ciclo de Vida Soluções AltoQi](https://suporte.altoqi.com.br/hc/pt-br/pol%C3%ADtica-de-ciclo-de-vida)
[](https://www.altoqi.com.br/home?_gl=1*apqakf*_gcl_au*NjY4MjI3ODQwLjE3NTkzMzAwNTcuNTI2MzMzOTU0LjE3NjIxOTQwNzcuMTc2MjE5NDExMA..*_ga*MTA2NDI3ODc1Ny4xNzYyMTkyMTE4*_ga_YWTWJ4QJW7*czE3NjIxOTIxMTgkbzckZzEkdDE3NjIxOTgwNDYkajI4JGwwJGgw*_ga_MSCRTLB9RC*czE3NjIxOTIxMTgkbzExJGcxJHQxNzYyMTk4MDQ2JGoyOCRsMCRoMA..)
Copyright © 2025 AltoQi. Todos os Direitos Reservados.
[Política de Privacidade](https://www.altoqi.com.br/politica-de-privacidade)