Faixas de Hillerborg: análises limites

Neste artigo, será abordado o método de Hillerborg para o cálculo de lajes. Diversos métodos aproximados de análise de lajes têm sido propostos, desenvolvidos e usados ao longo dos anos. Entre eles, está o conhecido método das faixas, apresentado por Hillerborg em 1956. Esse procedimento pode ser usado para determinar a distribuição de esforços e possibilitar o dimensionamento das seções de concreto e das armaduras de um sistema de lajes.

Análises limites

A Teoria Geral da Plasticidade demonstra que, devido à plasticidade, uma redistribuição dos momentos e esforços cortantes, pode ocorrer antes de ser atingida a carga última da laje. As análises limites procuram calcular a carga última da laje, assumindo que as seções da laje são suficientemente dúcteis para permitir a redistribuição necessária dos esforços. Entretanto podem ser usados métodos de dimensionamento baseados nos Teoremas Estáticos ou Cinemáticos.

O método baseado no Teorema Estático, também chamado limite inferior postula que:

1. As condições de equilíbrio devem ser satisfeitas para todos os pontos da laje;
2. O momento de plastificação da laje não pode ser excedido em nenhum ponto da laje;
3. Todas as condições de contorno são satisfeitas.

A carga assim calculada é a carga última. Isto significa que a carga última nunca é superestimada (o procedimento está sempre a favor da segurança em relação ao Estado Limite Último). Para todas as soluções possíveis de distribuição de momentos, antes da carga última da placa ser atingida, é necessária uma redistribuição de momentos, mesmo quando o dimensionamento é feito pela teoria elástica. Isso se deve ao fato de que a distribuição de momentos depende de uma distribuição complexa na rigidez da placa depois da fissuração do concreto. Portanto, as análises limites só podem ser aplicadas em lajes de concreto armado que possuam seções com grande ductilidade. Como foi demonstrado no Análise de placas pela Teoria da Elasticidade, a equação de equilíbrio de um elemento de placa é dada por:

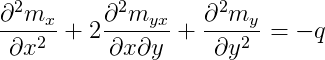
Esta equação pode ser aplicada tanto aos elementos de laje que estão em regime elástico, quanto em regime plástico, já que ela é deduzida apenas a partir de considerações de equilíbrio. Qualquer solução que satisfaça também as condições de contorno e o critério de plastificação é uma solução possível para a configuração de momentos. Portanto, existe um grande número de soluções entre as quais a teoria elástica é uma das possíveis.

Para obter-se as soluções possíveis, a carga q deve ser equilibrada pela soma dos termos do lado esquerdo da equação, onde o primeiro e o terceiro termo estão relacionados aos momentos fletores nas direções X e Y, que correspondem ao funcionamento de vigas; e o segundo termo está relacionado aos momentos de torção (ou volventes). O fato da carga da laje poder ser equilibrada por qualquer combinação de momentos fletores e de torção nas duas direções dá uma ideia clara do conceito físico do método.

O método das faixas de Hillerborg é o procedimento mais usado baseado em uma análise de limite inferior. Esse método obtém a distribuição de momentos e esforços cortantes através da substituição da laje por um sistema de faixas dispostas em duas direções, as quais dividem entre si as cargas aplicadas. Esse é um procedimento válido porque o carregamento é suportado inteiramente por flexão, e por essa razão as condições de equilíbrio estático são satisfeitas e nenhuma resistência por torção é necessária.

No próximo artigo da série, Faixas de Hillerborg: aplicação, mostrarei em maior detalhe como este método é aplicado.