Simular uma placa através de elementos de barras formando uma grelha, é um procedimento conhecido desde os primórdios da engenharia estrutural. A Analogia de Grelha foi usada por Euler em 1766 para a solução de problemas de membranas elásticas e por Hrennikoff em 1941 para a análise de placas através de uma formulação denominada Lattice Analogy.
Método dos deslocamentos aplicado a grelhas planas
Uma estrutura de grelha assemelha-se, em vários aspectos, a um pórtico plano. Todas as barras e nós existem no mesmo plano, supondo-se que as barras estão rigidamente ligadas nos nós (no caso de estrutura de nós rígidos). Os efeitos de flexão tendem a predominar na análise, sendo os efeitos de torção secundários, porém importantes. Na análise de uma de grelha, a estrutura existe no plano X-Y com todas as forças aplicadas atuando no eixo Z.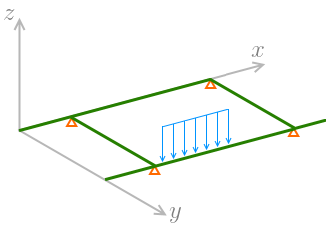 
Como cada elemento de uma grelha pode estar orientado em qualquer direção no plano XY, é conveniente que cada barra possua um sistema de eixos cartesianos ortogonais conhecido como eixo de coordenadas locais. Para o sistema local, os eixos denominados de xM, yM e zM estão dispostos da seguinte maneira:
-
xM coincide com o eixo da barra e com o sentido orientado do nó inicial j para o nó final k;
-
zM é perpendicular ao plano da grelha , dirigido para cima;
-
yM é orientado perpendicular ao plano formado pelos eixos xM e zM.
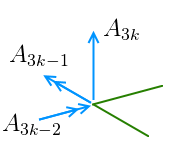
Os deslocamentos que podem ocorrer nos nós de uma estrutura são, basicamente duas translações e quatro rotações. Estes deslocamentos possíveis são chamados de graus de liberdade, ou seja, cada deslocamento possível de um nó é um grau de liberdade. Os deslocamentos possíveis nas extremidades de uma barra de grelha são mostrados na figura a seguir e consistem em quatro rotações nas direções X e Y e duas translações na direção Z.
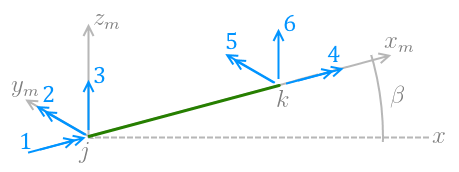
Matriz de rigidez das barras da grelha
Os deslocamentos unitários nas extremidades da barra podem ser provocados um de cada vez, com o objetivo de formar a matriz de rigidez da barra de grelha, relativa ao eixo local da barra. A matriz [K] é a matriz de rigidez da grelha. O significado físico de [K] pode ser descrito como:
"Cada coluna {j} da matriz [K] é um vetor de cargas que deve ser aplicado ao grau de liberdade de modo a manter o estado de deformação associado com um valor unitário do grau de liberdade j, enquanto todos os demais graus de liberdade são zero."
A seguir, serão apresentadas as fórmulas para o cálculo das ações nas extremidades das barras de grelha para os diversos deslocamentos impostos. Uma barra é restringida quando uma das suas extremidades é impedida de se deslocar, seja por translação ou rotação. As ações de extremidade para uma barra restringida são ações de reação, forças ou momentos, que aparecem nas extremidades quando a barra é submetida a esforços, variação de temperatura, deslocamentos impostos ou outros efeitos.
Na figura a seguir, temos o caso de uma barra com as duas extremidades engastadas, submetida a um deslocamento vertical Δ em uma das extremidades. Devido a este deslocamento, a barra fica submetida a esforços de reação nas extremidades. Se este deslocamento for unitário, estes esforços correspondem à rigidez da barra em relação a esse grau de liberdade.
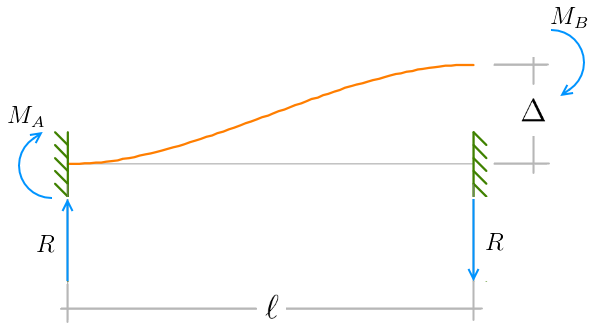
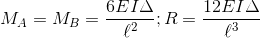
Abaixo, representamos o caso de uma barra com as duas extremidades engastadas, submetida a uma rotação ϕ ao redor do seu próprio eixo, em uma das extremidades. Devido a esta rotação, a barra reage com os momentos de torção Mt nas duas extremidades.
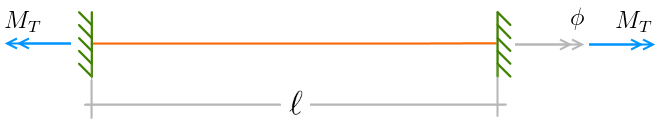
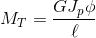
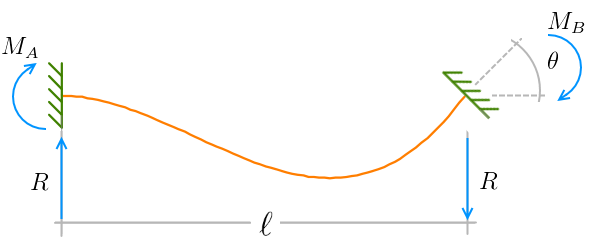
Já na figura abaixo, representamos o caso de uma barra com as duas extremidades engastadas, submetida a uma rotação θ em uma das extremidades. Devido a esta rotação, a barra reage com os momentos fletores MA e MB nas duas extremidades e com as duas reações R.
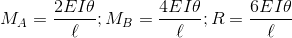
Estas ações de extremidade são suficientes para construir a matriz de rigidez de uma barra de grelha plana utilizada neste estudo. Outras análises mais sofisticadas poderiam incluir outros termos na matriz de rigidez a partir de efeitos específicos.
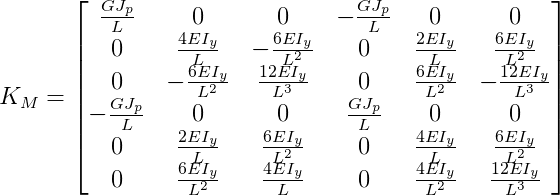
Os termos com GJp são os termos que representam a rigidez à torção das barras de grelha. Os demais termos referem-se à rigidez à flexão da barra.
Transformação das matrizes de rigidez dos elementos
A rotação de eixos para vetores no plano pode ser formulada em uma base geométrica através de dois sistemas de eixos coincidentes na origem rotacionados de um angulo β.
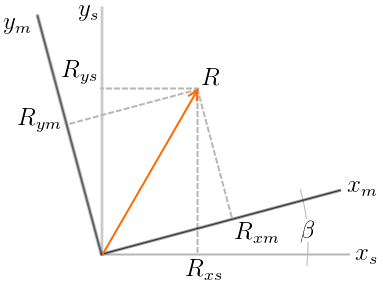
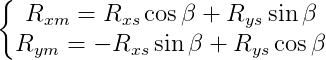
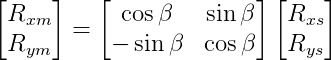
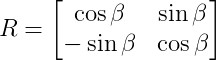
R é uma matriz de senos e co-senos que é denominada matriz de rotação.
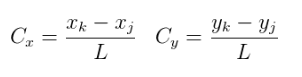Onde o comprimento da barra L pode ser calculado a partir das coordenadas dos nós extremos:
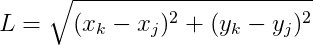
Denominando Cx = cosb e Cy = senb, a matriz de rigidez de barra de grelha, em relação aos eixos globais é:
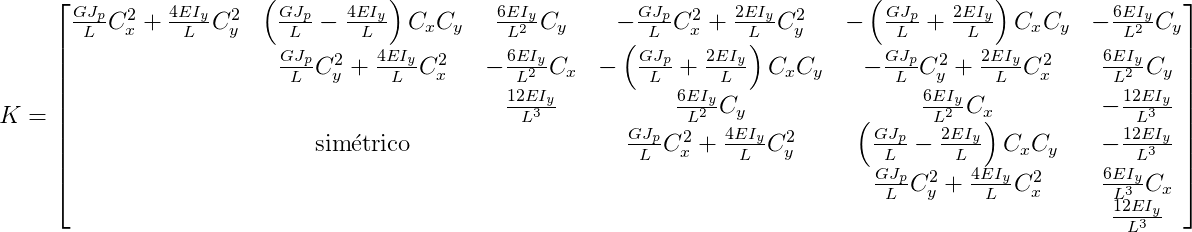
Após gerada a matriz de rigidez Ki de cada barra na forma expandida, os elementos desta matriz são transferidos para a matriz de rigidez de nós K da estrutura.
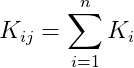
Este procedimento de somar diretamente as matrizes de rigidez dos elementos para formar a matriz de rigidez da estrutura é freqüentemente chamado de método direto da rigidez (direct stiffness method). O fato de se usar a ferramenta matemática de matrizes é o que leva muitas vezes o método de análise ser designado de análise matricial.
Esforços nodais aplicados
Na fase seguinte da análise, formam-se os vetores associados às cargas sobre a grelha. As ações externas aplicadas nos nós constituem o vetor A.
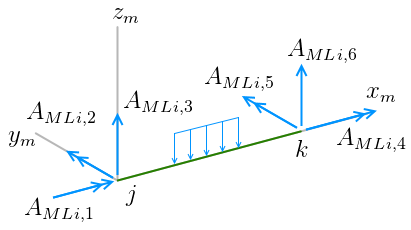
Com as ações AML nas extremidades de uma barra restringida da grelha (devido às cargas) constrói-se o vetor de cargas equivalentes Ae.
As cargas nodais reais, vetor A, podem ser somadas às cargas nodais equivalentes, vetor Ae, para produzir o vetor de cargas combinadas Ac.
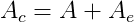
Note que o vetor Ac consiste em duas partes. A primeira parte representa a soma das cargas nodais reais e equivalentes correspondentes aos graus de liberdade conhecidos. A segunda parte, consiste na soma das cargas nodais reais equivalentes correspondentes às restrições de apoio sobre a estrutura. Se os sinais dos elementos desta parte de Ac forem invertidos, aparece o vetor ARL. O vetor de cargas combinadas está composto da seguinte maneira:
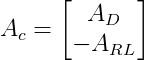
Como os efeitos das cargas sobre as barras foram colocados na forma de cargas nodais equivalentes, isto implica que o vetor ADL é nulo. Portanto, a equação:
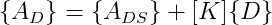
Pode ser simplificada para:
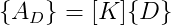
Cálculo dos deslocamentos e esforços nas barras
Na fase final da análise, as matrizes geradas na etapa anterior são substituídas nas equações apropriadas, com o propósito de calcular os deslocamentos nodais desconhecidos D, as reações AR e as ações de extremidade de barra AM. Os deslocamentos nodais desconhecidos são calculados com a equação:
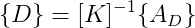
Existem diversas métodos para solucionar sistemas de equações lineares simultâneas, dentre os quais citamos o método de Cholesky. O objetivo desta solução é o vetor de deslocamentos nodais D da estrutura da grelha. Como estes deslocamentos estão referidos ao sistema de coordenadas globais podemos calcular os deslocamentos nodais referidos ao sistema local por meio da matriz de transformação de cada barra da grelha, e, com eles, obter os esforços nas extremidades da barra. As ações nas extremidades das barras AM podem ser obtidas com a equação:
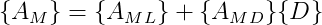
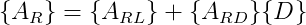
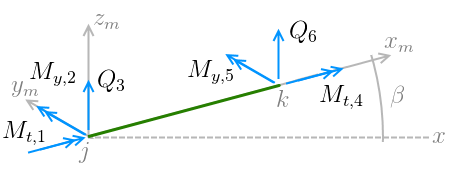
Onde MT são momentos de torção, MY momentos fletores no plano xmzm e Q os esforços cortantes no plano xmzm. No próximo artigo desta série, Influência da rigidez à torção no cálculo de lajes, irei abordar a influência desses momentos torsores no que diz respeito aos esforços da laje.