Exemplo de aplicação utilizando séries trigonométricas

Existem diversos procedimentos para a análise e dimensionamento de lajes em concreto armado. Dentre os vários  disponíveis estão a teoria elástica, a teoria da análise limite e as modificações da teoria da análise limite. Esses procedimentos podem ser usados para determinar os deslocamentos e os esforços nas lajes e nos elementos de apoio, bem como determinar a capacidade de carga última da laje.

Exemplo de aplicação utilizando séries trigonométricas

Neste artigo, vou mostrar um exemplo com a solução matemática exata de um problema de placa, conforme solucionado em TIMOSHENKO, S.P. & WOINOWSKY-KRIEGER, S. (1959). Trata-se de uma placa retangular com carregamento senoidal distribuído, escolhido justamente para que se possa ter uma solução da equação de Lagrange.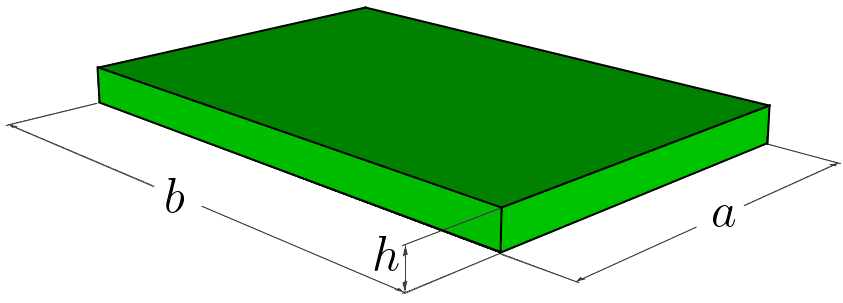 

Uma placa retangular, conforme apresentado, está sujeita a um carregamento distribuído sobre toda a superfície de acordo com a lei senoidal dada pela expressão, sendo q0 o valor máximo da carga no centro da placa.

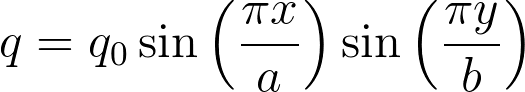
Substituindo este carregamento na equação de Lagrange obtém-se:

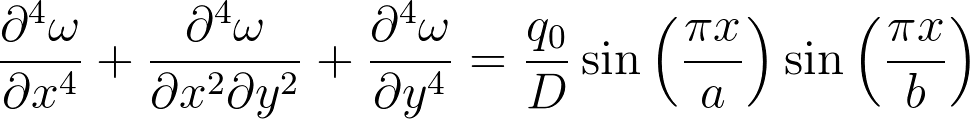
As condições de contorno para a placa simplesmente apoiada são mostradas abaixo:

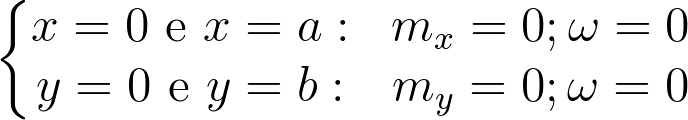
Usando as expressões para o cálculo dos momentos:

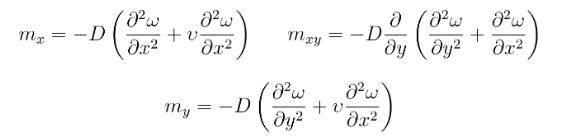 E, como ω = 0 nos bordos, tem-se a relação abaixo. Pode-se mostrar que, para os lados paralelos a X e Y, as condições de contorno são:

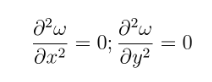
A solução para a equação de Lagrange que satisfaz todas as condições de contorno apresentadas, pode ser dada  por:

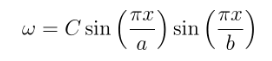
onde C é uma constante que deve satisfazer a equação de carregamento, a qual, substituída na equação de Lagrange, resulta em:

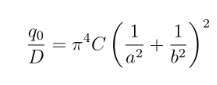
Obtém-se, então, um campo de deslocamentos, para a placa, dado por:

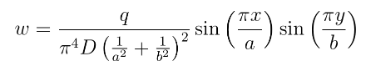
Com a expressão que define o campo de deslocamento e utilizando as equações que definem os momentos, obtém-se os campos de momentos fletores e de momentos de torção para a placa:

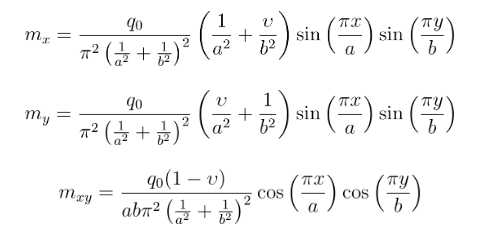
Como pode-se observar, mesmo a solução para um caso simples é bastante trabalhosa e precisa ser resolvida numericamente. A solução do problema de placas pelo caminho clássico é limitada a um número relativamente pequeno de geometria de placas, de carregamentos e condições de contorno. Se essas condições forem complexas, a análise em muitos casos é impraticável.

Como a equação de Lagrange é uma equação diferencial parcial de quarta ordem, torna-se muito difícil à solução de diversos casos práticos, especialmente quando os efeitos das deformações dos elementos de apoio precisam ser levados em consideração.

Entretanto, diversas técnicas de análise foram desenvolvidas para obter essas soluções, em especial o uso de computadores e o Método das Diferenças Finitas e o Método dos Elementos Finitos permitem que soluções da teoria elástica possam ser obtidas para sistemas de lajes com qualquer carregamento e quaisquer condições de contorno.