Análise de placas pela Teoria da Elasticidade

Existem diversos procedimentos para a análise e dimensionamento de lajes em concreto armado. Dentre os vários  disponíveis estão a teoria elástica, a teoria da análise limite e as modificações da teoria da análise limite. Esses procedimentos podem ser usados para determinar os deslocamentos e os esforços nas lajes e nos elementos de apoio, bem como determinar a capacidade de carga última da laje.

Análise de placas pela Teoria da Elasticidade

A Teoria da Elasticidade, na qual foi inicialmente baseado o cálculo de placas, é, como o nome diz, uma teoria elástica, cujas hipóteses básicas variam de acordo com o tipo de placa considerada. No caso de placas de pouca espessura, como a maioria das lajes de edifícios, as hipóteses básicas, conforme TIMOSHENKO, S.P. & WOINOWSKY-KRIEGER, S. (1959) e SZILARD, Rudolph (1974), são as seguintes:

• o material da placa é elástico, homogêneo e isotrópico;

• a placa indeformada é plana;

• a espessura (h) da placa é pequena em relação às outras dimensões (da ordem de 1/10);

• as deformações angulares da superfície média são pequenas comparadas à unidade;

• os deslocamentos dos pontos da superfície média são pequenos comparados com a espessura da placa (inferiores a 1/10, para que se possa considerar pequenas deformações);

• as cargas dinâmicas ou estáticas são aplicadas perpendicularmente à superfície da placa;

• a configuração deformada da placa é tal que linhas retas inicialmente perpendiculares à superfície média permanecem retas e perpendiculares;

• as deformações devidas ao cisalhamento são desprezadas;

• a deformação da placa é produzida por deslocamentos dos pontos da superfície média perpendicular ao plano indeformado;

• as tensões normais à superfície média são desprezíveis em relação às tensões no mesmo plano.

Usando estas hipóteses e considerando um elemento de placa de dimensões dx e dy submetido a uma carga distribuída q, o equilíbrio é obtido a partir dos esforços internos atuantes: momentos fletores mx e my, momentos de torção mxy e myx e esforços cortantes qx e qy , atuando nas faces do elemento.

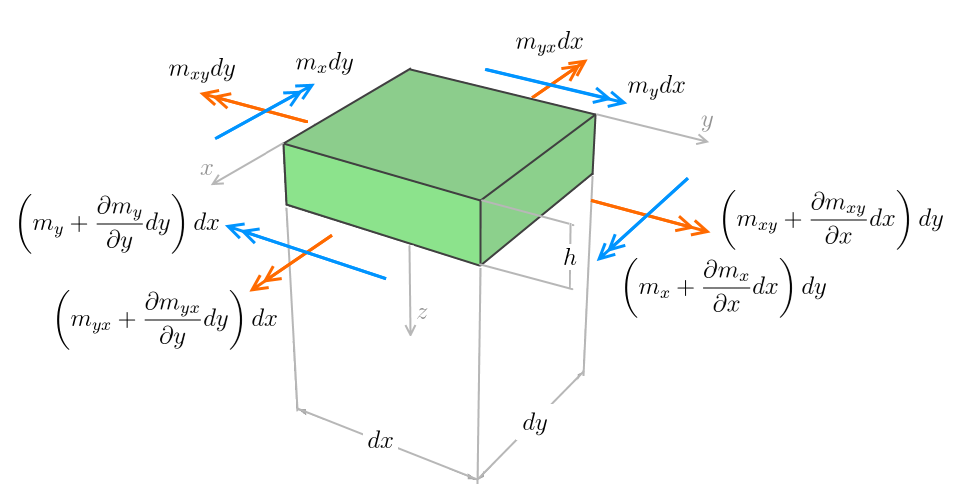
Deste equilíbrio de forças, obtemos as equações abaixo, conhecidas como equações diferenciais das placas em regime elástico:

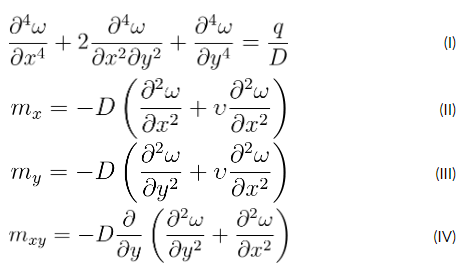
Onde q é a carga distribuída na placa por unidade de área, E o módulo de elasticidade do material da placa (módulo de Young), h a espessura da placa, υ o coeficiente de Poisson, e D a  rigidez da placa, que é dada pela equação abaixo:

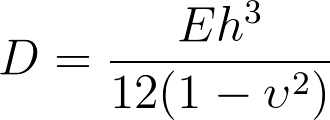
A equação (I) é a equação diferencial das placas, ou equação de Lagrange, em coordenadas cartesianas retangulares. Ela define o campo de deslocamentos da placa ω em função das coordenadas x,y, da carga q e da rigidez D da placa. Portanto, os deslocamentos da laje calculados pela Teoria da Elasticidade dependem da dimensão da placa, das condições de contorno, do carregamento, do módulo de elasticidade E do material (constante), da espessura da placa e do coeficiente de Poisson.

Uma outra equação importante é obtida a partir do equilíbrio de um elemento de placa, submetido a uma carga distribuída q. O equilíbrio é conseguido com os esforços internos atuantes: momentos fletores mx e my , os momentos de torção mxy e myx  e os esforços cortantes qx e qy, atuando nas faces do elemento.

 

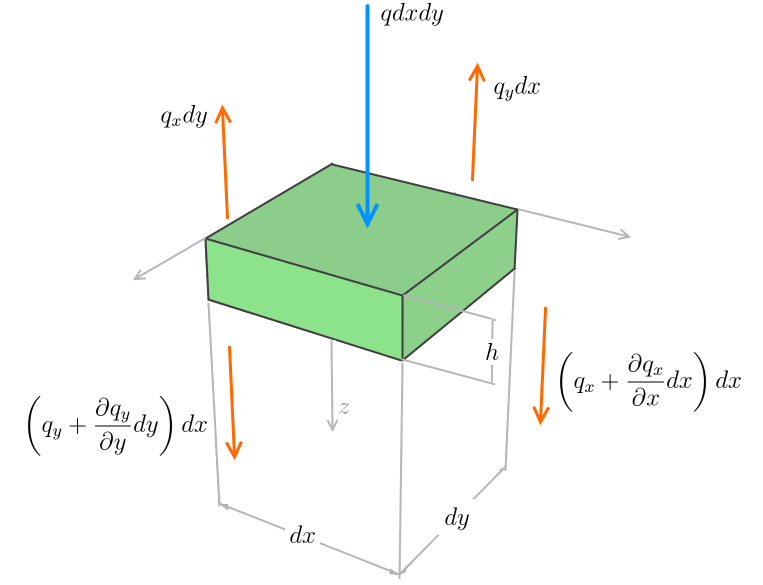
Obtém-se a equação (V), que estabelece o equilíbrio das placas. É muito importante notar que esta equação é independente do fato de a placa estar em regime elástico ou plástico, independente do coeficiente de Poisson e se a placa é isotrópica ou ortotrópica.

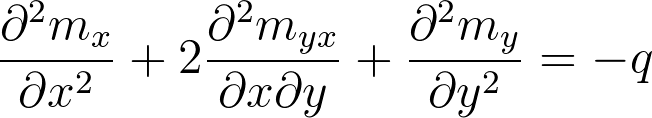
A solução exata fechada de placas, obtida algebricamente através da solução destas equações diferenciais, é restrita a poucos casos e, portanto, tem pouca finalidade prática. Outras soluções matemáticas numéricas disponíveis para o problema de placas são:

• solução por séries simples;

• solução por séries duplas trigonométricas (conhecida por solução de Navier).

No artigo Exemplo de aplicação utilizando séries trigonométricas será mostrado um exemplo de como este cálculo deve ser realizado.