Pilares estão superdimensionados

Em alguns casos, é possível que o lance superior de um pilar apresente uma bitola, ou número de barras, maior do que no lance abaixo.

Pilares estão superdimensionados

Conforme destacado no artigo anterior desta série, de modo geral, pilares devem trabalhar com um esforço axial preponderante. De todo modo, nem sempre é este o caso: o dimensionamento de pilares envolve diversos tópicos da engenharia estrutural tais como análise não-linear, estabilidade global e dimensionamento de seções de concreto armado. Por conta disto, em determinadas situações de projeto, pode-se obter uma variação considerável do quantitativo de barras em um pilar, de acordo com o lance de prumada analisado. 

Uma forma de avaliar por que um pilar pode ser mais armado que outro é através de parâmetros adimensionais, como por exemplo a força normal adimensional υ e a excentricidade e. A força normal adimensional υ indica a taxa de compressão do pilar, ou seja, a relação entre o esforço normal máximo solicitante e o esforço normal resistente:

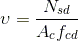
A excentricidade de um pilar pode ser definida como a razão entre o seu momento fletor e o esforço normal à que é submetido: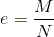 

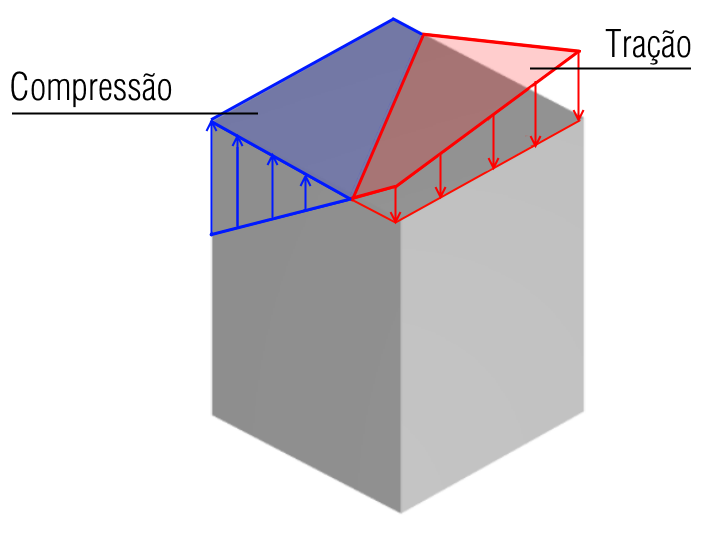
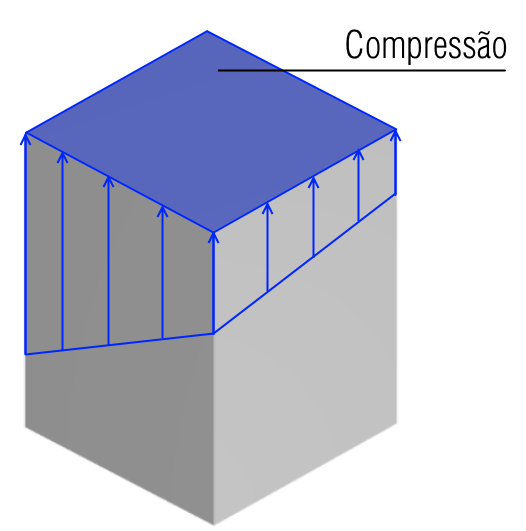
Quando um pilar tem valores baixos de taxa de compressão (υ < 0.2) e valores elevados de excentricidade, o seu dimensionamento tende a ser mais crítico. Nestes casos, a seção de concreto não se encontra tão comprimida quanto poderia, visto que a taxa de compressão é pequena. Isto faz com que os momentos aplicados (excentricidade alta) tracionem uma certa região do concreto. Como a resistência à tração do concreto não é satisfatória, estes esforços devem ser resistidos pelas armaduras do pilar, o que implica em um dimensionamento mais robusto.

Ábacos de dimensionamento

Para expor este conceito de uma maneira mais formal, podemos lançar mão de ábacos de dimensionamento. Como exemplo, vamos utilizar um dos ábacos desenvolvidos por Libânio Pinheiro, Lívio Baraldi e Marcelo Porem da Escola de Engenharia de São Carlos:

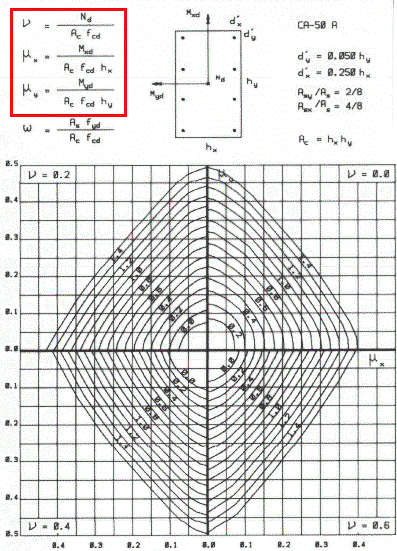
Perceba que, apesar de não citar excentricidades, o ábaco acima solicita, além da taxa de compressão, dois coeficientes: μx e μy. Estes dois coeficientes estão associados aos momentos agindo sobre a seção do pilar, de modo que contêm informações sobre as excentricidades relacionadas ao pilar em cada uma de suas direções:

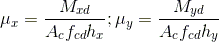
Para verificar este efeito, podemos então fixar os momentos do pilar, variando a sua taxa de compressão. Tomaremos então υ = 0.0 e υ = 0.2, que corresponde à parte superior do ábaco:

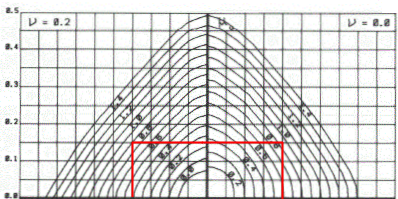
Perceba que, para os mesmos momentos temos ω = 0.8 e ω = 0.95, para os valores de υ = 0.2 e υ = 0.0, respectivamente. A partir destes valores, podemos calcular a área de aço da seção de acordo com a equação abaixo:

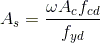
A área de aço definida para a seção aumenta proporcionalmente à ω. Desta maneira, quando analisamos os dois casos acima, podemos perceber que, ao considerar um pilar submetido apenas a momentos fletores, sem nenhuma carga axial (υ = 0.0), obtém-se uma área de aço maior do que quando se considera uma pequena carga axial (υ = 0.2) nesta mesma seção.  Deste modo, é fácil perceber porque um pilar em um pavimento de cobertura submetido a esforços relativamente pequenos pode ser dimensionado com uma quantidade significativa de armadura.

Assim, você pode optar por realizar alterações na concepção de modo que os momentos não sejam tão expressivos em pilares que possuem cargas axiais reduzidas. Neste sentido, recomendamos a leitura do artigo Como reduzir a armadura de pilares?. Em contrapartida, é também possível uniformizar a armadura dos pilares, procedimento que é o assunto do próximo artigo dessa série.