Método do pilar padrão acoplado a diagramas momento curvatura

Ao realizar o dimensionamento de pilares através do AltoQi Eberick, diversos critérios normativos são considerados para compensar possíveis imperfeições geométricas, efeitos de segunda ordem e excentricidades devido à fluência do concreto.

Momentos de segunda ordem pelos diagramas M, N, 1/r

Para determinação dos momentos de segunda ordem locais durante o dimensionamento de pilares no AltoQi Eberick, são utilizados os métodos aproximados prescritos na norma. Os dois métodos apresentados anteriormente, da curvatura aproximada e rigidez aproximada, utilizam expressões simplificadas para parâmetros importantes desta análise. O método do pilar padrão acoplado a diagramas M, N, 1/r, por sua vez, é um método onde a rigidez do pilar é obtida graficamente de um diagrama momento - carga normal - curvatura (M, N, 1/r) obtido para a situação específica do pilar. Este método está prescrito no item 15.8.3.3.4 da norma NBR 6118:2014. 

O diagrama momento-curvatura deve sempre ser determinado para cada direção, na situação específica do pilar. Por este motivo, a utilização do diagrama momento-curvatura representa um método mais preciso que os métodos anteriores, podendo portanto ser aplicado para pilares com λ ≤ 140. Como nos métodos anteriores, no entanto, este método ainda é um método simplificado, e portanto conforme a norma NBR 6118:2014 só pode ser aplicado para pilares com seção e armadura constante em todo o eixo.

A determinação do diagrama momento-curvatura é um processo que necessita de uma análise iterativa, devendo portanto ser realizado computacionalmente, por tentativas ou aproximações sucessivas. Após possuir o diagrama momento-curvatura do pilar, é possível obter-se graficamente a rigidez secante através do diagrama. A figura 15.1 da norma mostra a obtenção deste valor:

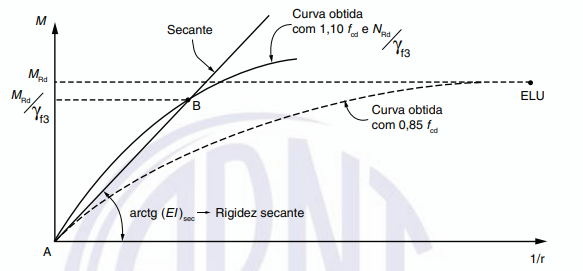
 Desta forma, conhecendo-se a rigidez secante, pode-se determinar uma rigidez secante adimensional κsec através da seguinte expressão:

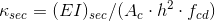
onde,

Com esta rigidez definida, obtém-se o momento solicitante de cálculo com a consideração do efeito de segunda ordem através da seguinte expressão:

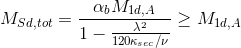
onde,

Desta forma, obtém-se o valor do momento solicitante com consideração dos efeitos de segunda ordem através do método do pilar padrão acoplado a diagramas M, N, 1/r.

Este artigo finaliza a apresentação dos métodos de determinação dos esforços de segunda ordem nesta série de artigos. Os próximos artigos desta série irão apresentar outros critérios para a obtenção do momento solicitante para o dimensionamento, e finalmente o processo de dimensionamento de pilares pelo programa.

Referências

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto - Procedimento. Rio de Janeiro, 2014.