Influência da rigidez à torção no cálculo de lajes

Simular uma placa através de elementos de barras formando uma grelha, é um procedimento conhecido desde os primórdios da engenharia estrutural. A Analogia de Grelha foi usada por Euler em 1766 para a solução de problemas de membranas elásticas e por Hrennikoff em 1941 para a análise de placas através de uma formulação denominada Lattice Analogy.

Influência da rigidez à torção no cálculo de lajes

A aplicação da Analogia de Grelha para o cálculo de lajes em princípio parece tratar-se da simples aplicação do programa de análise de grelhas planas com o painel discretizado. Os resultados dos esforços e deslocamentos obtidos seriam então usados para o dimensionamento. No entanto, é necessário analisar a influência dos diversos parâmetros nos resultados, tais como número de faixas, rigidez a flexão e a torção entre outras. No modelo de grelhas planas os esforços nas extremidades das barras que correspondem aos graus de liberdade são os seguintes:

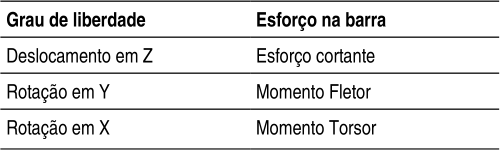
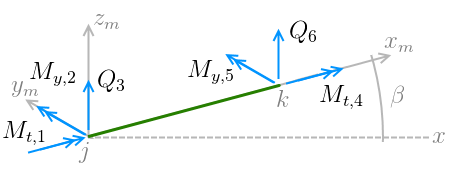
Estes esforços são proporcionais às rigidezes correspondentes das barras, que na matriz das barras são parâmetros de rigidez a torção GJp e  de rigidez a flexão EIy.

O parâmetro de rigidez a torção GJp é composto do módulo de elasticidade transversal G do material, que pode ser medido ou calculado em função do módulo de elasticidade transversal Ec ou módulo de Young e do momento de inércia polar Jp da seção transversal da barra. Para materiais isotrópicos homogêneos, a lei de Hooke generalizada possui apenas três constantes elásticas E, ν e  G.  A equação de conexão é:

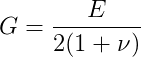
Para aplicações em concreto armado, a NBR 6118/1980 no item 8.2.6 fixa o valor do coeficiente de Poisson em 0.2, adotando-se a seguinte relação aproximada:  

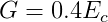
O outro parâmetro é o momento de inércia polar da seção transversal da barra Jp. As barras da grelha possuem seção retangular com largura igual a largura das faixas e altura igual a espessura da placa. O momento de inércia pode então ser calculado conforme GERE e WEAVER (1980) pela fórmula:

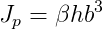
onde:

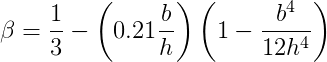
Nessas fórmulas, b é sempre a menor dimensão. Portanto quando as faixas possuírem largura maior que a altura, o valor b é igual a espessura da faixa e h igual a largura da faixa. Quando as faixas passam  a ter uma largura menor que a espessura da placa, esta situação inverte-se.

No último artigo da série, Exemplo: cálculo de uma grelha, irei mostrar um exemplo de cálculo de grelha, onde foram utilizadas vigas para representar as faixas de concreto. Neste artigo, será mais visível a influência deste momento torsor nos demais esforços.